010 - Nonlinear torsion

3 min read • 465 words

Test of the Wagner strain term with standard 6-DOF frame elements.

e0010.py

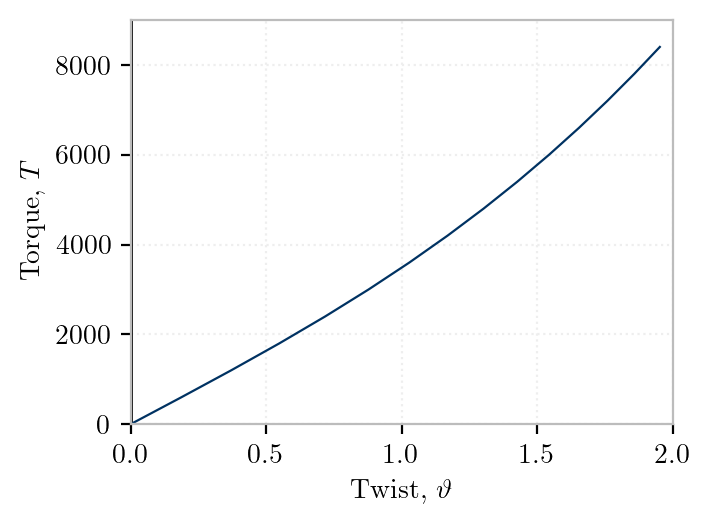
The torque-twist rotation behavior of a cantilever torsion member of narrow rectangular section $200 \mathrm{~mm} \times 10 \mathrm{~mm}$ is shown in Fig. 1. The member has a concentrated torque $M$ acting at the righthand end and is prevented from rotating at the left-hand support. The beam properties are $G=80,000 \mathrm{MPa}, E=200,000 \mathrm{MPa}, J$ $=66.667 \mathrm{E} 3 \mathrm{~mm}^4, I_w=0 \mathrm{~mm}^6, I_n=17.778 \mathrm{E} 9 \mathrm{~mm}^6$ , and length $L$ $=1,000 \mathrm{~mm}$ .

This beam is in uniform torsion under a constant torque $M_z$ $=M$ , so that the twist $d \phi / d z$ is constant along the member. In this case, Eq. (1) can be solved in closed form as

M=G J \frac{\phi_L}{L}+\frac{1}{2} E I_n\left(\frac{\phi_L}{L}\right)^3

where $\phi_L=$ twist rotation at the free end.

Rectangle, pure torsion (no instability), unconstrained warping, .

Nonuniform constrained warping was considered by

Wen Yi Lin; Kuo Mo Hsiao. (2001). Co-rotational formulation for geometric nonlinear analysis of doubly symmetric thin-walled beams. , 190(45), 6023–6052. doi:10.1016/s0045-7825(01)00212-2
@trahair2005nonlinear
Battini et al. (2002a), example 7.4
@du2021threedimensional

python (collapsed)

# Test of the Wagner strain term.
# Battini et al. (2002a), Example 7.4
#
import veux
from shps.shapes import Rectangle
import opensees.openseespy as ops
import matplotlib.pyplot as plt
try:
    pass
    plt.style.use("veux-web")
except:
    pass

def create_cantilever(element, section):

    d  = 10
    b  = .5

    E = 2.1e6 # MPa
    v = 0.33 #0.5*E/G - 1
    G = 0.5*E/(1+v) # 787500

    L  = 100
    ne =  5 # 20

    model = ops.Model(ndm=3, ndf=6)

    mat = 1
    sec = 1
    model.material('ElasticIsotropic', mat, E, v)

    shape = Rectangle(d=d, b=b).create_shape()

    if section == "Elastic":
        cmm = shape.torsion.cmm()
        cnn = shape.torsion.cnn()
        cnv = shape.torsion.cnv()
        cnm = shape.torsion.cnm()
        cmw = shape.torsion.cmw()
        A = cnn[0,0]
        model.section("ElasticFrame", sec,
                        E=E,
                        G=G,
                        A=A,
                        Ay=1*A,
                        Az=1*A,
                        Qy=cnm[0,1],
                        Qz=cnm[2,0],
                        Iy=cmm[1,1],
                        Iz=cmm[2,2],
                        J =shape.torsion.torsion_constant(),
                        Ry= cnv[1,0],
                        Rz=-cnv[2,0],
                        Sy= cmw[1,0],
                        Sz=-cmw[2,0]
        )
    else:
        model.section("ShearFiber", 1, GJ=0)
        for fiber in shape.fibers():
            y, z = fiber.location
            model.fiber(y, z, fiber.area, material=mat, warp=[fiber.warp[0], [0,0,0], [0,0,0]], section=1)

    model.geomTransf("Linear", 1, (0,0,1))

    model.node(0, (0,0,0))
    for i in range(ne):
        model.node(i+1, ((i+1)*L/ne, 0, 0))
        model.element(element, i+1, (i, i+1), section=1, transform=1)

    model.fix(0,  (1,1,1,  1,1,1))
    return model, shape


if __name__ == "__main__":
    import os
    import sys

    model, shape = create_cantilever(
                      section = os.environ["Section"],
                      element = os.environ.get("Element", "ExactFrame")
                   )
    end = len(model.getNodeTags()) - 1

    # MODEL DONE
    artist = veux.create_artist(model, model_config=dict(extrude_outline=shape))
    artist.draw_surfaces()
    artist.draw_outlines()

    # Apply torsional moment
    nsteps =  15
    Mmax   = 9e3
    model.pattern("Plain", 1, "Linear")
    model.load(end, (0,0,0,  1,0,0), pattern=1)

    model.system('Umfpack')
    model.integrator("LoadControl", Mmax/nsteps)
    model.test("NormDispIncr",1e-8,100,1)
#   model.test('NormUnbalance',1e-6,10,1)
    model.algorithm("Newton")
    model.analysis("Static")

    u = []
    P = []
    while model.getTime() < Mmax:
        u.append(model.nodeDisp(end, 4))
        P.append(model.getTime())
        if model.analyze(1) != 0:
            print(f"Failed at time = {model.getTime()}")
            break


    fig, ax = plt.subplots()
    ax.set_xlabel(r"Twist, $\vartheta$")
    ax.set_ylabel("Torque, $T$")
    ax.set_xlim([0,    2])
    ax.set_ylim([0, Mmax])
    ax.axvline(0, color='black', linestyle='-', linewidth=1)
    ax.axhline(0, color='black', linestyle='-', linewidth=1)
    ax.plot(u, P)

    plt.show()
#   plt.savefig("img/e0010.png")

    artist.draw_sections(state=model.nodeDisp)
    if len(sys.argv) > 1:
        artist.save(sys.argv[1])
    else:
        veux.serve(artist)

References

Drucker–Prager Triaxial Test

011 - Restrained torsion