020 - Follower loading

This example demonstrates the simulation of follower loading applied to frame elements.

This example demonstrates the simulation of follower loading applied to frame elements. Our model is a basic cantilever composed of ne, ExactFrame elements.

In order to define the follower loading, we first add a Plain  load pattern to the current Model  instance, labeled with the tag 1 and scaled in time by a Linear time series:

    model.pattern("Plain", 1, "Linear")

Next we add a FrameLoad  to this pattern, applied to the element with tag ne (ie, the last element).

model.eleLoad("Frame", "Dirac",
                  force = [0, 1, 0],
                  basis = "director",
                  offset=[1.0,0,0],
                  pattern=1,
                  elements=[ne]
)

pattern Plain 1 Linear 
eleLoad Frame Dirac -force {0 1 0} -basis director -offset {1.0 0 0} -pattern 1 -elements {10}

The argument "Dirac" specifies that the loading is Dirac delta function. Before performing the analysis, we’ll also define a Motion with the veux library which we will use to animate the simulation:

import veux
artist = veux.create_artist(model, model_config=dict(extrude_outline="square"))
artist.draw_nodes(size=10)
artist.draw_sections()
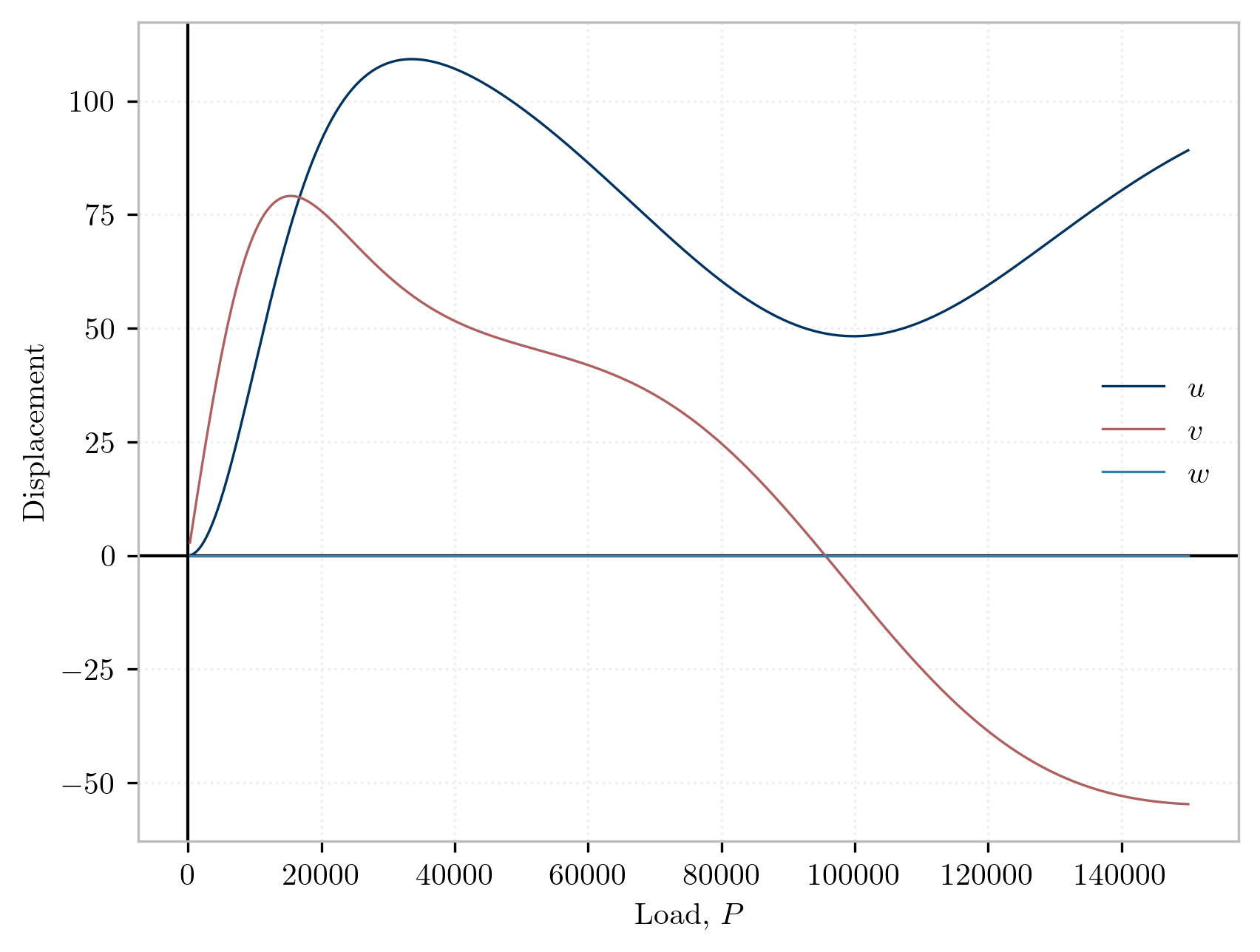
motion = veux.Motion(artist)

Once the loading is defined and post-processing is setup, the analysis procedure follows the standard idiom for static incremental analysis:

u = []
v = []
w = []
P = []
while model.getTime() < Pmax:
    if model.analyze(1) != 0:
        print(f"Failed at time = {model.getTime()} with v = {v[-1]}")
        break

    motion.advance(time=model.getTime()*speed)
    motion.draw_sections(rotation=model.nodeRotation,
                         position=model.nodeDisp)
    u.append(-model.nodeDisp(ne, 1))
    v.append( model.nodeDisp(ne, 2))
    w.append( model.nodeDisp(ne, 3))
    P.append( model.getTime())

The following plot reproduces Figure 4 from

References