Finite Rotations

3 min read • 482 words

This problem highlights the exceptional accuracy of the ExactFrame formulation for simulating large deformations

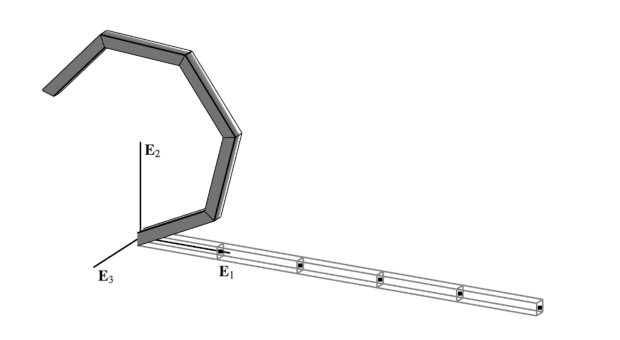
The cantilever beam depicted above is investigated; first under the action of a point moment $\boldsymbol{M}$ , then a point force $F \, \mathbf{E}_3$ at its free end $\xi=L$ . The reference curve of the reference configuration is given by $\boldsymbol{x}_0(\xi) = \xi\,\mathbf{E}_1$ .

In order to simulate this problem with OpenSees the ExactFrame  element formulation is used. This element requires a shear-deformable section, like ShearFiber  .

End Moment  

When $F = 0$ the configuration is expected to remain in the $\mathbf{E}_1 - \mathbf{E}_2$ plane. Consequently, the out-of-plane director $\mathbf{D}_3$ does not change during deformation so that $\mathbf{d}_3 = \mathbf{D}_3$ . This simplification has two important consequences:

• There is no distinction between a spatially applied moment $\boldsymbol{M} = M \, \mathbf{d}_3$ and a materially applied moment $\boldsymbol{M} = M \, \mathbf{D}_3$ .

• The rotation $\boldsymbol{\Lambda}$ becomes vectorial, its variations $\boldsymbol{u}_{\scriptscriptstyle{\Lambda}}^{(i)}$ at different configurations $\chi^{(i)}$ can be added, and the sum of these variations over the course of global equilibrium iterations is equivalent to the logarithmic rotation increment:

  $$\sum_{i=0}^n \boldsymbol{u}_{\scriptscriptstyle{\Lambda}}^{(i)} \equiv \boldsymbol{\theta} = \operatorname{Log} \left(\boldsymbol{\Lambda}_{(n)}\boldsymbol{\Lambda}_{(0)}^{\mathrm{t}}\right).$$

In this case, the moment loading can be treated identically for all analyses by simply scaling a constant reference force vector for the node at $\xi=L$ :

$$\mathbf{f}_{M,\text{ref}} = \begin{pmatrix} 0 & 0 & M \end{pmatrix}^{\mathrm{t}}$$

where the reference magnitude $M = \lambda 2 \pi EI/L$ varies with $\lambda=1/8, \ 1$ , and $2$ for different cases causing the cantilever to loop over itself $\lambda$ times. The following parameters are used:

$$\begin{array}{lcr} L &=& 10\hphantom{..} \\ E &=& 10^4 \\ G &=& 10^4 \\ \end{array} \qquad\qquad \begin{array}{lcr} A &=& 1\hphantom{..} \\ I &=& 10^{-2} \\ J &=& 10^{-2} \\ \end{array}$$

The analytic solution of the governing boundary value problem is given by:

$$\left\{ \begin{aligned} \boldsymbol{x}(\xi)&=\frac{EI}{M} \sin \vartheta(\xi) \, \mathbf{E}_1 + \frac{EI}{M}\left(\cos \vartheta(\xi)-1\right) \, \mathbf{E}_2 \\ \vartheta(\xi) &= \xi \frac{M}{EI} \end{aligned} \right.$$

where $\vartheta$ parameterizes the rotation $\boldsymbol{\Lambda}(\xi) = \operatorname{Exp} \vartheta(\xi) \, \mathbf{E}_3$ .

The simulation uses a single load step with uniform meshes of 5 elements for the 2-node and 3-node variants of all formulations investigated by . The solution requires only two iterations for each formulation matching the ideal performance reported by .

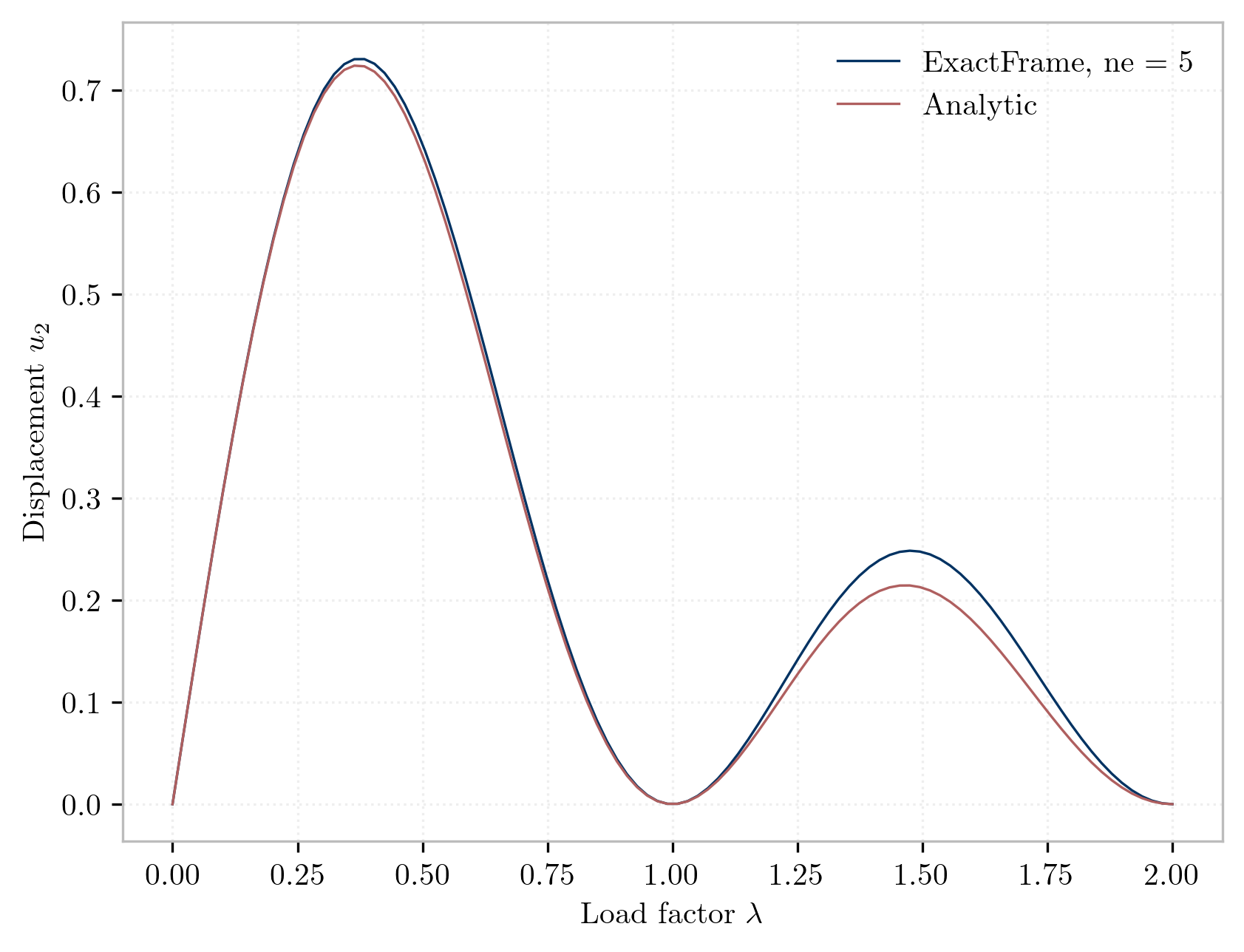
The tip displacements for the case $\lambda = 1/8$ are collected below. The displacements for $n=2$ -node elements match exactly those reported by for both the natural None, and the logarithmic Init/Incr variants. For $n=3$ -node elements, the results match the analytic solution up to the reported precision.

References  

• NAFEMS Finite Element Methods & Standards, Abbassian, F., Dawswell, D. J., and Knowles, N. C., Selected Benchmarks for Non-Linear Behavior of 3D-Beams. Glasgow: NAFEMS, Publication NNB, Rev. 1, Oct. 1989. Test NL5.

• Abaqus NL5 

• https://classes.engineering.wustl.edu/2009/spring/mase5513/abaqus/docs/v6.6/books/bmk/default.htm?startat=ch02s01ach122.html 

• https://manuals.dianafea.com/d100/FXpDia/node221.html