Arch Instability
5 min read • 1,061 wordsSeveral nonlinear static analysis methods are used to investigate instabilities in a shallow arch.
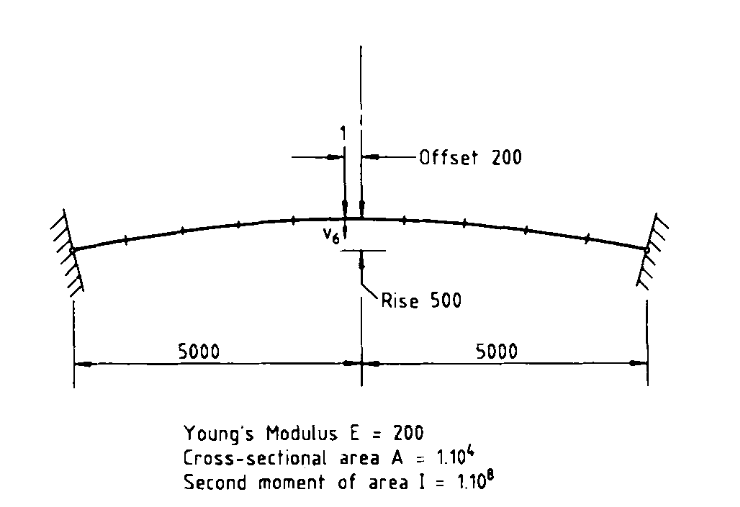
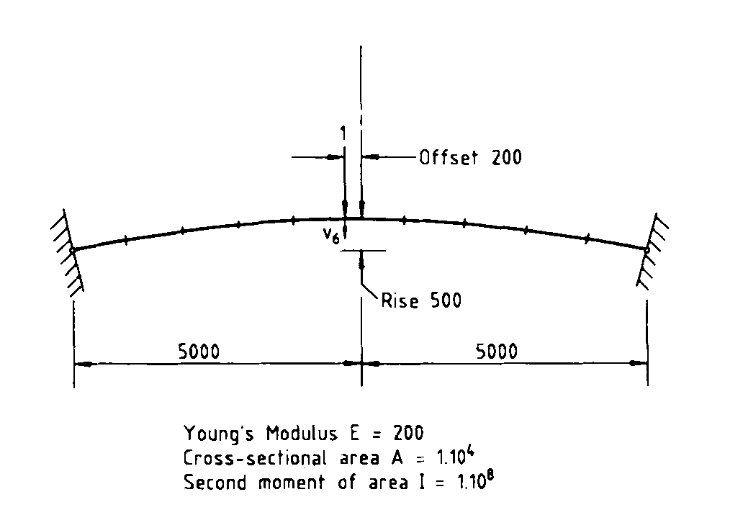In this problem, we investigate how this programmatic interface can be used to solve a highly nonlinear problem. Consider the shallow arch shown above (Clarke and Hancock, 1990).
This problem exhibits several critical points along the solution path, and requires the use of a sophisticated algorithm to properly traverse these. In this study, we will investigate how the OpenSees framework can be used to compose these algorithms.
We will perform the analysis by creating a xara.Model object, and using
its methods to perform various tasks. A method is simply a function that
is linked to a particular instance of a data structure. In this case, the Model
data structure holds the geometry and state (i.e., the current values of solution variables) of our structural model. Some methods that you might see being used in this notebook include (you wont need to make any changes to the use of any of these):
-
Model.integrator(...)This method configures the iteration strategy to be performed in the next increment -
Model.analyze(n)This method appliesnincrements, and between each increment, performs Newton-Raphson iterations.
In this notebook, the Model data structure is created by the arch_model helper function, which we load from the file
arch.py:
from arch import arch_modelWe’ll also find the following imports convenient:
import numpy as np
import matplotlib.pyplot as plt
try:
import scienceplots
plt.style.use(["steel"]) #(["ieee", "science", "notebook"])
except:
passSolution Strategy
Our general strategy is implemented in the following function solve().
This function adopts an incremental approach
where the load is applied in small steps of varying size.
The arguments to the function are:
model: axara.Modelobjectnode: an integer indicating which node to collect results from.
Both of these arguments will be supplied by the arch_model helper function mentioned
above.
def analyze(model, mid, increment, steps, dx, *args):
# Initialize some variables
xy = [] # Container to hold solution history (i.e., load factor and displacement at `node`)
status = 0 # Convergence flag; Model.analyze() will return 0 if successful.
# Configure the first load increment strategy; explained below
increment(model, dx, *args)
for step in range(steps):
# 1. Perform Newton-Raphson iterations until convergence for 1 load
# increment
status = model.analyze(1)
# 2. Store the displacement and load factor
xy.append([model.nodeDisp(mid, 2), model.getTime()])
# 3. If the iterations failed, try cutting
# the increment arc-length in half
if status != 0:
dx /= 2
increment(model, dx, *args)
return np.array(xy).TThe strategies used by Clarke and Hancock are:
- Solution 1
-
Iterative strategy: Constant load (Section 3.1)
Load incrementation strategy: Direct incrementation of the load parameter (Section 4.1.1) - Solution 2
-
Iterative strategy: Constant vertical displacement under the load, $u_{\mathrm{mid}}$ (Section 3.2)
Load incrementation strategy: Incrementation of the displacement component $u_{\mathrm{mid}}$ (Section 4.1.2) - Solution 3
-
Iterative strategy: Constant arc-length (Section 3.3)
Load incrementation strategy: Incrementation of the arc-length (Section 4.1.3) - Solution 4
-
Iterative strategy: Minimum unbalanced displacement norm (Section 3.5)
Load incrementation strategy: Incrementation of the arc-length (Section 4.1.3) - Solution 5
-
Iterative strategy: Constant weighted response (Section 3.7, equation (39))
Load incrementation strategy: Incrementation of the arc-length (Section 4.1.3) - Solution 6
-
Iterative strategy: Minimum unbalanced force norm (Section 3.6)
Load incrementation strategy: Using the current stiffness parameter (Section 4.2, equation (57)) - Solution 7
-
Iterative strategy: Minimum unbalanced force norm (Section 3.6)
Load incrementation strategy: Incrementation of the arc-length (Section 4.1.3) - Solution 8
-
Iterative strategy: Constant arc-length (Section 3.3)
Load incrementation strategy: Using the current stiffness parameter (Section 4.2, equation (57))
def solution0(model, dx):
model.integrator("LoadControl", 400.0)
def solution1(model, dx):
Jd = 5
model.integrator("LoadControl", dx, Jd, -800., 800.)
def solution2(model, dx, *args):
Jd = 5
mid, dof = args
model.integrator("DisplacementControl", mid, dof, dx, Jd)
def norm_control(model, dx, *args):
Jd = 15
model.integrator("MinUnbalDispNorm", dx, Jd, -10, 10, det=True)
def arc_control(model, dx, *args, a=0):
model.integrator("ArcLength", dx, a, det=True, exp=0.0, reference="point")fig, ax = plt.subplots()
# x, y = solution0(*arch_model(), 6, 400.0)
# ax.plot(-x, y, 'x', label="S0")
# x, y = analyze(*arch_model(), solution1, 6, 400.0)
# ax.plot(-x, y, 'x', label="S1")
# print(y)
model, mid = arch_model()
x, y = analyze(model, mid, solution2, 7, -150, *(mid, 2))
ax.plot(-x, y, 'o', label="S2")
x, y = analyze(*arch_model(), solution2, 536, -1.5, *(mid, 2))
ax.plot(-x, y, '-', label="S2")
# x, y = analyze(*arch_model(), arc_control, 9500, 0.5, 0)
# ax.plot(-x, y, "-", label="arc")
x, y = analyze(*arch_model(), arc_control, 110, 45)
ax.plot(-x, y, "x", label="arc")
# x, y = analyze(*arch_model(), arc_control, 80, 88, 0)
# ax.plot(-x, y, "+", label="arc")
# x, y = analyze(*arch_model(), arc_control, 80, 188, 0)
# ax.plot(-x, y, "*", label="arc")
# x, y = analyze(*arch_model(), arc_control, 8000, 0.8, 0)
# ax.plot(-x, y, "x", label="arc")
# x, y = analyze(*arch_model(), norm_control, 7000, 1.0)
# ax.plot(-x, y, "-", label="norm")
ax.set_title("Displacement vs Load Factor")
ax.set_ylabel(r"Load factor $\lambda$")
ax.set_xlabel("Displacement $u$")
ax.set_xlim([0, 1200])
ax.set_ylim([-800, 3000])
fig.legend();
fix, ax = plt.subplots()
ax.plot(-x, '.');
ax.set_title("Displacement vs Step Number")
ax.set_ylabel("Displacement $u$")
ax.set_xlabel("Analysis step $n$");
The following animation of the solution is created in
Animating.ipynb
References
Clarke, M.J. and Hancock, G.J. (1990) ‘A study of incremental‐iterative strategies for non‐linear analyses’, International Journal for Numerical Methods in Engineering, 29(7), pp. 1365–1391. Available at: https://doi.org/10.1002/nme.1620290702 .
The source code for creating the arch structure is given below:
import numpy as np
import opensees.openseespy
# Create the model
def arch_model():
# Define model parameters
L = 5000
Rise = 500
Offset = 200
# Compute radius
R = Rise/2 + (2*L)**2/(8*Rise)
th = 2*np.arcsin(L/R)
#
# Build the model
#
model = opensees.openseespy.Model(ndm=2, ndf=3)
# Create nodes
ne = 10
nen = 2 # nodes per element
nn = ne*(nen-1)+1
mid = (nn+1)//2 # midpoint node
for i, angle in enumerate(np.linspace(-th/2, th/2, nn)):
tag = i + 1
# Compute x and add offset if midpoint
x = R*np.sin(angle)
if tag == mid:
x -= Offset
# Compute y
y = R*np.cos(angle)
# create the node
model.node(tag, x, y)
# Define elastic section properties
E = 200
A = 1e4
I = 1e8
model.section("ElasticFrame", 1, A=A, E=E, I=I)
# Create elements
transf = 1
model.geomTransf("Corotational", transf)
for i in range(ne):
tag = i+1
nodes = (i+1, i+2)
model.element("PrismFrame", tag, nodes, section=1, transform=transf)
model.fix( 1, 1, 1, 0)
model.fix(nn, 1, 1, 0)
# Create a load pattern that scales linearly
model.pattern("Plain", 1, "Linear")
# Add a nodal load to the pattern
model.load(mid, 0.0, -1.0, 0.0, pattern=1)
# Select linear solver, and ensure determinants are
# computed and stored.
# model.system("ProfileSPD")
# model.system("FullGeneral")
# model.system("BandGeneral")
model.system("Umfpack", det=True)
model.test("NormUnbalance", 1e-6, 25, 9)
model.algorithm("Newton")
model.analysis("Static")
return model, mid