Finite Rotations

3 min read • 598 words

This problem highlights the exceptional accuracy of the ExactFrame formulation for simulating large deformations

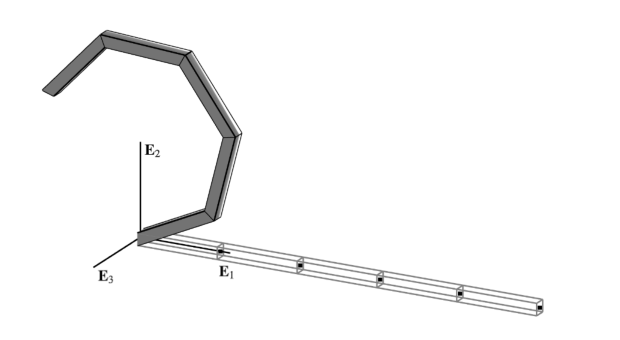
The cantilever beam depicted above is investigated. First under the action of a point moment $\boldsymbol{M}$ , then a point force $F \, \mathbf{E}_3$ at its free end $\xi=L$ . The reference curve of the reference configuration is given by $\boldsymbol{x}_0(\xi) = \xi\,\mathbf{E}_1$ .

End Moment  

When $F = 0$ the configuration is expected to remain in the $\mathbf{E}_1 - \mathbf{E}_2$ plane. Consequently, the out-of-plane director $\mathbf{D}_3$ does not change during deformation so that $\mathbf{d}_3 = \mathbf{D}_3$ . This simplification has two important consequences:

• There is no distinction between a spatially applied moment $\boldsymbol{M} = M \, \mathbf{d}_3$ and a materially applied moment $\boldsymbol{M} = M \, \mathbf{D}_3$ .

• The rotation $\boldsymbol{\Lambda}$ becomes vectorial, its variations $\boldsymbol{u}_{\scriptscriptstyle{\Lambda}}^{(i)}$ at different configurations $\chi^{(i)}$ can be added, and the sum of these variations over the course of global equilibrium iterations is equivalent to the logarithmic rotation increment:

  $$\sum_{i=0}^n \boldsymbol{u}_{\scriptscriptstyle{\Lambda}}^{(i)} \equiv \boldsymbol{\theta} = \operatorname{Log} \left(\boldsymbol{\Lambda}_{(n)}\boldsymbol{\Lambda}_{(0)}^{\mathrm{t}}\right).$$

In this case, the moment loading can be treated identically for all analyses by simply scaling a constant reference force vector for the node at $\xi=L$ :

$$\mathbf{f}_{M,\text{ref}} = \begin{pmatrix} 0 & 0 & M \end{pmatrix}^{\mathrm{t}}$$

where the reference magnitude $M = \lambda 2 \pi EI/L$ varies with $\lambda=1/8, \ 1$ , and $2$ for different cases causing the cantilever to loop over itself $\lambda$ times. The following parameters are used:

$$\begin{array}{lcr} L &=& 10\hphantom{..} \\ E &=& 10^4 \\ G &=& 10^4 \\ \end{array} \qquad\qquad \begin{array}{lcr} A &=& 1\hphantom{..} \\ I &=& 10^{-2} \\ J &=& 10^{-2} \\ \end{array}$$

The analytic solution of the governing boundary value problem is given by:

$$\left\{ \begin{aligned} \boldsymbol{x}(\xi)&=\frac{EI}{M} \sin \vartheta(\xi) \, \mathbf{E}_1 + \frac{EI}{M}\left(\cos \vartheta(\xi)-1\right) \, \mathbf{E}_2 \\ \vartheta(\xi) &= \xi \frac{M}{EI} \end{aligned} \right.$$

where $\vartheta$ parameterizes the rotation $\boldsymbol{\Lambda}(\xi) = \operatorname{Exp} \vartheta(\xi) \, \mathbf{E}_3$ .

The simulation uses a single load step with uniform meshes of 5 elements for the 2-node and 3-node variants of all formulations investigated by . The solution requires only two iterations for each formulation matching the ideal performance reported by .

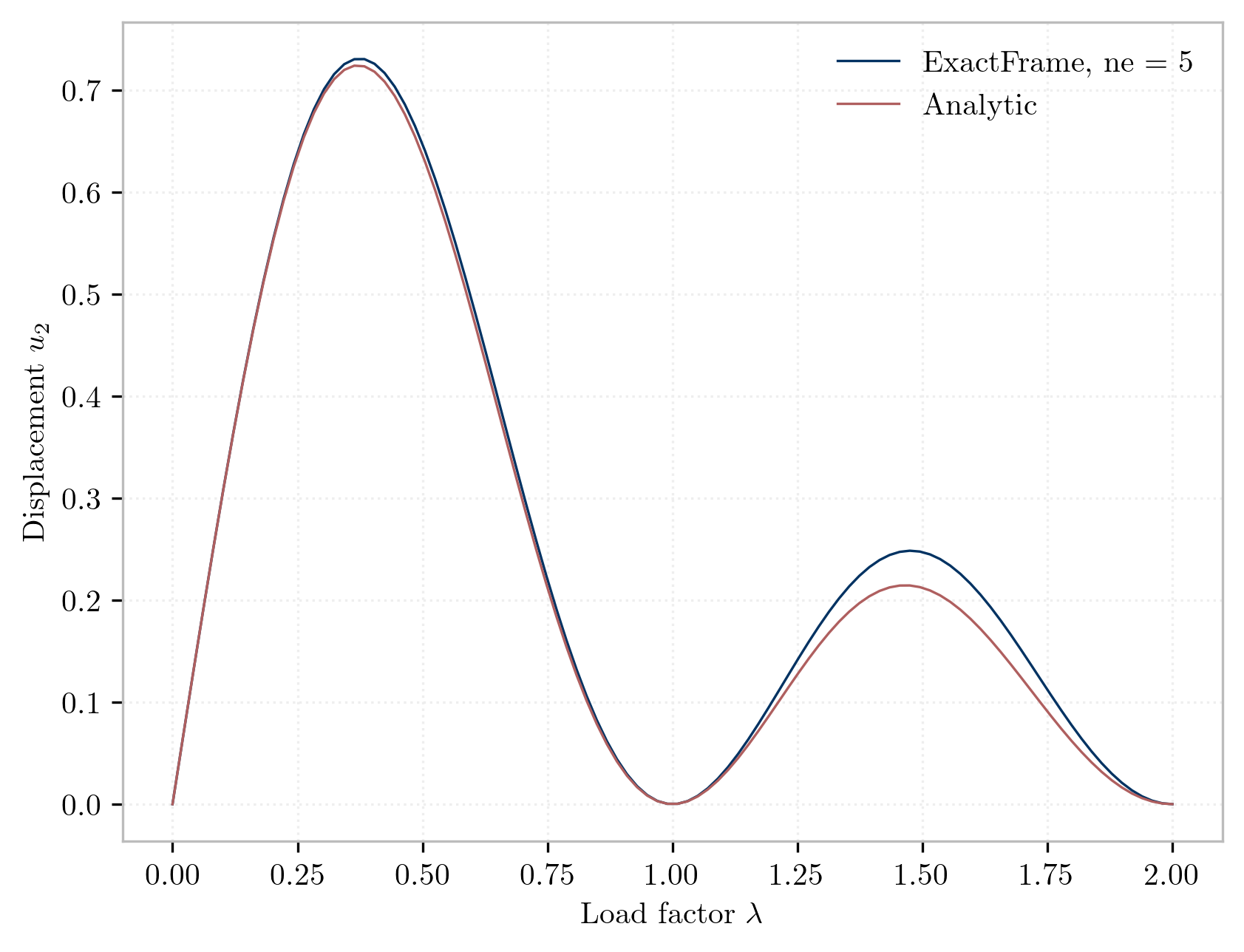
The tip displacements for the case $\lambda = 1/8$ are collected below. The displacements for $n=2$ -node elements match exactly those reported by for both the natural None, and the logarithmic Init/Incr variants. For $n=3$ -node elements, the results match the analytic solution up to the reported precision.

End Force  

In this case the cantilever beam is subjected only to a transverse force of $\boldsymbol{F} = 10 \, \mathbf{E}_2$ in a single step. The simulation uses the following geometric and material properties from the literature:

$$\begin{array}{lr} L =& 1 \\ E =& 10 \\ \hphantom{.} \end{array} \qquad \begin{array}{lr} A =& 10^7 \\ I =& 1 \\ J =& 10^7 \\ \end{array}$$

Two values for the shear modulus $G$ are used with a shear stiffness $GA$ of $500$ and $10$ , respectively, the latter representing the case with significant shear deformations. Table (#tab:transv) presents the numerical tip displacements and the analytic solution from using Jacobi elliptic functions and accounting for flexural and shear deformations. The analysis uses both 2-node and 4-node elements. For the sake of brevity, the results are reported only for the variants using the same parameterization as the wrapped element’s interpolation.

In order to simulate this problem with OpenSees the ExactFrame  element formulation is used. This element requires a shear-deformable section, like ShearFiber  .

References