Helical Forms

A highly geometrically nonlinear problem is solved with the geometrically exact frame element formulation.

A cantilever beam is subjected to a combined point moment $\boldsymbol{M}$ and a point force $F \, \mathbf{E}_3$ at its free end $\xi=L$ . This example is selected to demonstrate the ability of the proposed formulations to naturally accommodate applied moments in various reference frames. It also highlights the accuracy and convergence characteristics of the formulations. Three common variations of this problem are considered with the following properties:

The ExactFrame  element formulation from OpenSees is employed.

Simple Perturbation  

Following , the problem of plane flexure with finite rotations is now altered by introducing the point load $\boldsymbol{F} = 1/16 \, \mathbf{E}_3$ in addition to the moment $\boldsymbol{M}$ so as to induce a three-dimensional response. A uniform mesh of 10, 2-node elements is used, and the reference moment from this study with $\lambda = 1/8$ is applied in a single load step. Because the deformation is no longer plane, each choice of nodal parameterization essentially equilibriates the moment in a different coordinate system. Results are reported in Table  tab:helical-perturb01, where the None/None/None and Incr/None/Incr variants match the values reported by for the formulations by and , respectively. Once again, the application of external isometry or parameter transformations does not affect the convergence characteristics of the solution.

Consistent Perturbation  

The problem is simulated again, but now the moment is consistently applied with a spatial orientation. Formulations whose final residual moment vector is conjugate to the spatial variations $\boldsymbol{u}_{\scriptscriptstyle{\Lambda}}$ of the rotation $\boldsymbol{\Lambda}$ do not need to be treated differently. This includes both elements with the None parameter transformation and transformed elements with the Petrov-Galerkin formulation. For the simulations with all other elements, a transformation of the nodal force is necessary, as described in . Table  tab:helical-perturb02 lists the tip displacements for the solution.

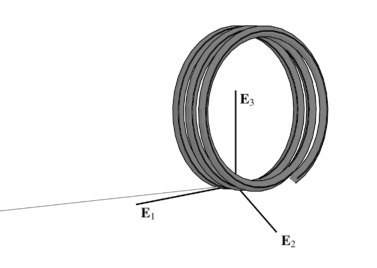
Oscillating Spiral  

To demonstrate the behavior of the proposed formulations under large rotations, the reference moment value $M$ in is now increased to $\lambda=10$ with a large out-of-plane force of $F=5 \lambda$ . The model discretization uses 100 two-node elements, and the loading is applied in 200 steps under load factor control. Figures below show the final deformed shape alongside a plot of the tip displacement in the direction of the concentrated force. These results are in agreement with the literature . See also

References