Truss Domes
6 min read • 1,272 wordsSeveral periodic truss domes are generated using OpenSeesRT.
A variety of periodic truss structures are investigated. This class of
models was investigated by .
All figures have been produced with
veux
.
The following code block contains the source code used to generate these
models. In particular, the function revolve() takes a representative segment
and generates a full model by revolving the nodes and elements.
# ===----------------------------------------------------------------------===//
#
# OpenSees - Open System for Earthquake Engineering Simulation
# Structural Artificial Intelligence Laboratory
# gallery.stairlab.io
#
# ===----------------------------------------------------------------------===//
"""
References
==========
Koohestani, K., and A. Kaveh.
“Efficient Buckling and Free Vibration Analysis of Cyclically Repeated Space Truss Structures.”
Finite Elements in Analysis and Design 46, no. 10 (October 2010): 943–48. https://doi.org/10.1016/j.finel.2010.06.009.
"""
from math import pi, sin, cos, sqrt
import opensees.openseespy as ops
def create_dome(design: str, *args, **kwds):
return _DOMES[design](*args, **kwds)
def dome52():
"""
References
==========
Degertekin, S.O., G. Yalcin Bayar, and L. Lamberti.
“Parameter Free Jaya Algorithm for Truss Sizing-Layout Optimization under Natural Frequency Constraints.”
Computers & Structures 245 (March 2021): 106461. https://doi.org/10.1016/j.compstruc.2020.106461.
"""
pass
def dome120():
"""
Create a segment of the 120-bar dome. Use with revolve() to generate
a full structural model as follows:
nodes, elems = revolve(*dome120())
References
==========
Lieu, Qui X., Dieu T. T. Do, and Jaehong Lee.
“An Adaptive Hybrid Evolutionary Firefly Algorithm for Shape and Size Optimization of Truss Structures with Frequency Constraints.”
Computers & Structures 195 (January 15, 2018): 99–112. https://doi.org/10.1016/j.compstruc.2017.06.016.
Kaveh, A., and M. Ilchi Ghazaan.
“Optimal Design of Dome Truss Structures with Dynamic Frequency Constraints.”
Structural and Multidisciplinary Optimization 53, no. 3 (March 1, 2016): 605–21. https://doi.org/10.1007/s00158-015-1357-2.
"""
# Number of repeated segments
s = 12
# Number of nodes per segment
n = 4
scale = 1/100
r1 = 273.26*scale
r2 = 492.12*scale
r = 625.59*scale
h = 275.59*scale
h1 = 196.85*scale
h2 = 118.11*scale
c2 = cos(pi/s)
s2 = sin(pi/s)
nodes = {
0: ( 0 , 0.0 , h ),
1: ( r1, 0.0 , h1),
2: ( r2, 0.0 , h2),
3: ( r , 0.0 , 0 ),
4: (r2*c2, r2*s2, h2),
}
elems = [
(0, 1),
(1, 2),
(2, 3),
(3, 4),
(2, 4),
(1, 4),
(1+n, 4),
(1+n, 1),
(3+n, 4),
(2+n, 4),
(1+n, 4)
]
return nodes, elems, {3}, s, {0}
def dome600():
"""
Create a segment of the 600-bar dome. Use with revolve() to generate
a full structural model as follows:
nodes, elems = revolve(*dome600())
References
==========
Kaveh, Ali, Kiarash Biabani Hamedani, and Bamdad Biabani Hamedani.
“Optimal Design of Large-Scale Dome Truss Structures with Multiple Frequency Constraints Using Success-History Based Adaptive Differential Evolution Algorithm.”
Periodica Polytechnica Civil Engineering, September 28, 2022. https://doi.org/10.3311/PPci.21147.
"""
# Number of repeated segments
s = 24
# Number of nodes per segment
n = 9
nodes = {
1: ( 1.0, 0.0, 7.0) ,
2: ( 1.0, 0.0, 7.5) ,
3: ( 3.0, 0.0, 7.25) ,
4: ( 5.0, 0.0, 6.75) ,
5: ( 7.0, 0.0, 6.0) ,
6: ( 9.0, 0.0, 5.0) ,
7: (11.0, 0.0, 3.5) ,
8: (13.0, 0.0, 1.5) ,
9: (14.0, 0.0, 0.0)
}
elems = [
(1, 2),
(1, 3),
(1, 1+n),
(1, 2+n),
(2, 3),
(2, 2+n),
(3, 2+n),
(3, 3+n),
(3, 4),
(4, 3+n),
(4, 4+n),
(4, 5),
(5, 4+n),
(5, 5+n),
(5, 6),
(6, 5+n),
(6, 6+n),
(6, 7),
(7, 6+n),
(7, 7+n),
(7, 8),
(8, 7+n),
(8, 8+n),
(8, 9),
(9, 8+n)
]
return nodes, elems, {9}, s, {}
def dome1180():
"""
Create a segment of the 1180-bar dome. Use with revolve() to generate
a full structural model as follows:
nodes, elems = revolve(*dome1180())
Kaveh, Ali, Kiarash Biabani Hamedani, and Bamdad Biabani Hamedani. “Optimal Design of Large-Scale Dome Truss Structures with Multiple Frequency Constraints Using Success-History Based Adaptive Differential Evolution Algorithm.” Periodica Polytechnica Civil Engineering, September 28, 2022. https://doi.org/10.3311/PPci.21147.
Kaveh, Ali, and M. Ilchi Ghazaan. “Optimal Design of Dome Truss Structures with Dynamic Frequency Constraints.” Structural and Multidisciplinary Optimization 53, no. 3 (March 1, 2016): 605–21. https://doi.org/10.1007/s00158-015-1357-2.
"""
s = 20
n = 20
nodes = {
1: ( 3.1181, 0.0 , 14.6723),
2: ( 6.1013, 0.0 , 13.7031),
3: ( 8.8166, 0.0 , 12.1354),
4: (11.1476, 0.0 , 10.0365),
5: (12.9904, 0.0 , 7.5000),
6: (14.2657, 0.0 , 4.6358),
7: (14.9179, 0.0 , 1.5676),
8: (14.9179, 0.0 , -1.5677),
9: (14.2656, 0.0 , -4.6359),
10: (12.9903, 0.0 , -7.5001),
11: ( 4.5788, 0.7252, 14.2657),
12: ( 7.4077, 1.1733, 12.9904),
13: ( 9.9130, 1.5701, 11.1476),
14: (11.9860, 1.8984, 8.8165),
15: (13.5344, 2.1436, 6.1013),
16: (14.4917, 2.2953, 3.1180),
17: (14.8153, 2.3465, 0.0),
18: (14.4917, 2.2953, -3.1181),
19: (13.5343, 2.1436, -6.1014),
20: ( 3.1181, 0.0 , 13.7031)
}
elems = [
(i, i+1) for i in range(1, 10)
] + [
(i, i+n) for i in range(1, 10)
] + [
(i, i+9) for i in range(2, 10)
] + [
(i, i+10) for i in range(2, 10)
] + [
(i+n, i+9) for i in range(2, 10)
] + [
(i+n, i+10) for i in range(2, 10)
]
return nodes, elems, {None}, s, {}
def dome1410():
"""
Create a segment of the 1410-bar dome. Use with revolve() to generate
a full structural model as follows:
nodes, elems = revolve(*dome1410())
Koohestani, K., and A. Kaveh.
“Efficient Buckling and Free Vibration Analysis of Cyclically Repeated Space Truss Structures.” Finite Elements in Analysis and Design 46, no. 10 (October 2010): 943–48. https://doi.org/10.1016/j.finel.2010.06.009.
"""
s = 30
n = 13
nodes = {
1: ( 1.0,0.0,4.0) ,
2: ( 3.0,0.0,3.75) ,
3: ( 5.0,0.0,3.25) ,
4: ( 7.0,0.0,2.75) ,
5: ( 9.0,0.0,2.0) ,
6: (11.0,0.0,1.25) ,
7: (13.0,0.0,0.0),
8: ( 1.989,0.209, 3.0),
9: ( 3.978,0.418,2.75),
10: ( 5.967,0.627,2.25),
11: ( 7.956,0.836,1.75),
12: ( 9.945,1.0453,1.0),
13: (11.934,1.2543,-0.5)
}
elems = [
( 1, 2),
( 2, 3),
( 3, 4),
( 4, 5),
( 5, 6),
( 6, 7),
( 8, 9),
( 9, 10),
(10, 11),
(11, 12),
(12, 13),
( 8+n, 8),
( 9+n, 9),
(10+n, 10),
(11+n, 11),
(12+n, 12),
(13+n, 13),
( 7, 13),
( 7+n, 13)
]
for i in range(2, 7):
elems.extend([(i , i+6),
(i , i+7),
(i+n, i+6),
(i+n, i+7)])
return nodes, elems, {None}, s, {}
_DOMES = {
"600": dome600,
"120": dome120,
"1410": dome1410,
"1180": dome1180
}
def revolve(ref_nodes, ref_elems, fixed, count, key_nodes=None, scale=1, shift=None):
"""
Create nodes and connectivity of a structure that is generated by revolving a
reference assembly idenfied by ref_nodes and ref_elems.
wr
"""
nodes = {}
elems = []
if key_nodes is None:
key_nodes = set()
nn = len(ref_nodes) - len(key_nodes)
for i in range(count):
angle = 2*pi*i/count
cs = cos(angle)
sn = sin(angle)
if 0 in ref_nodes:
node = ref_nodes[0]
nodes[0] = (cs*node[0] - sn*node[1],
sn*node[0] + cs*node[1],
node[2])
# Create nodes
for j,node in ref_nodes.items():
if j : # not in key_nodes:
nodes[j+i*nn] = (cs*node[0] - sn*node[1],
sn*node[0] + cs*node[1],
node[2])
for elem in ref_elems:
elems.append(tuple(
node if node in key_nodes else (node-1+i*nn)%(count*nn)+1 for node in elem
))
return nodes, elems
def create_truss(nodes, elems, areas=None):
"""
Create a truss model in OpenSees
"""
# Create a model in 3 dimensions with 3 degrees of freedom
model = ops.Model(ndm=3, ndf=3)
# Define a linear-elastic material
model.uniaxialMaterial('Elastic', 1, 3000)
area = 1.0
# Add nodes to the model
for tag, node in nodes.items():
model.node(tag, node)
# Add elements to the model
for tag, nodes in enumerate(elems):
model.element("Truss", tag, nodes, area, 1)
return model
if __name__ == "__main__":
import veux
nodes, elems = revolve(*dome1180())
model = create_truss(nodes, elems)
artist = veux.render(model, vertical=3)
# Show the rendering
veux.serve(artist)
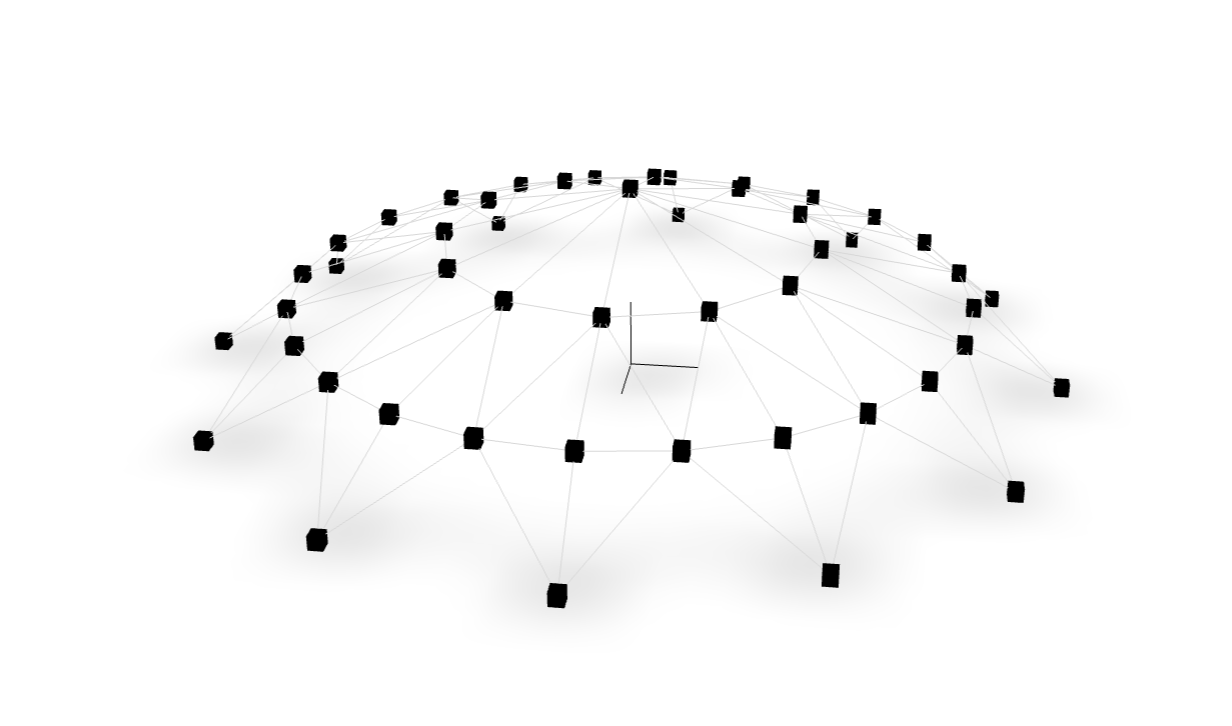 This model is investigated by .
This model is investigated by .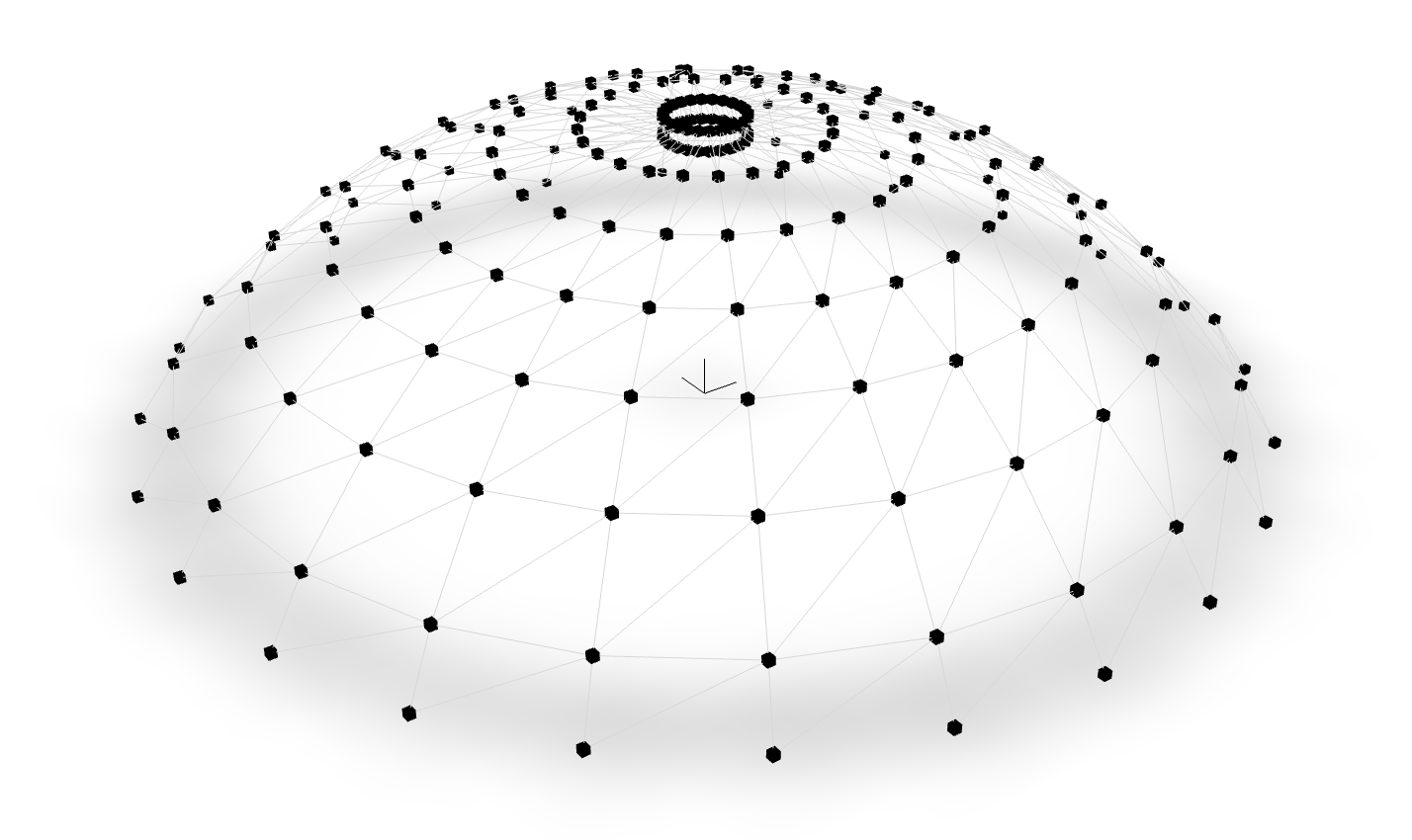 This model is investigated by
This model is investigated by
