Wrench
4 min read • 730 wordsStatic analysis of a wrench
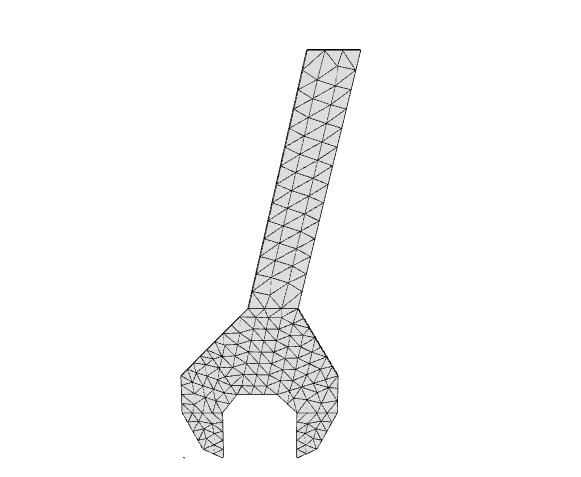
This problem is adapted from Logan (2012), Problem 7–28.
The problem is implemented for both quadrilateral and triangular finite elements.
In both versions the surface method is used, but extra work is required for triangles.
For the triangular mesh, the
Tri31
element is used.
# ===----------------------------------------------------------------------===//
#
# OpenSees - Open System for Earthquake Engineering Simulation
# Structural Artificial Intelligence Laboratory
# stairlab.berkeley.edu
#
# ===----------------------------------------------------------------------===//
#
# Static analysis of a wrench in the plane.
#
# The mesh is created from 7 blocks:
# ______
# / /
# / /
# / /
# / /
# / /
# / /
# / /
# / /
# / 7 /
# /_____/ ____
# / \
# / 6 \ 70
# /_____________\ ____
# | \ / |
# | \ 3 / | 20
# | 4 \_______/ 2 | _________
# |___/ \___| ____ 20
# \5 | | 1/ 70
# \_| |_/ __
# . o ____ __ 10
# ^
# #
#
# Chrystal Chern and Claudio Perez
#
import veux
import opensees.openseespy as ops
import numpy as np
a = np.arctan(1/5)
# Quadrilateral blocks that comprise the wrench:
blocks = {
1: {
1: [ 0, 0],
2: [ 20, 10],
3: [ 40, 160-70-40],
4: [ 0, 160-70-40],
6: [ 35, 30]},
# 6: [ 25, 30]},
2: {
1: [ 0, 160-70-40],
2: [ 40, 160-70-40],
# 6: [ 45, 160-70-20],
3: [ 40, 160-70 ],
4: [ -20, 160-70-20]},
3: {
1: [ -20, 160-70-20],
2: [ 40, 160-70 ],
3: [-115, 160-70 ],
4: [ -60, 70]},
4: {
1: [ -60, 70],
2: [-115, 90],
3: [-115, 50],
4: [ -75, 50]},
5: {
1: [ -75, 50],
2: [-115, 50],
3: [ -95, 10],
4: [ -75, 0]},
6: {
1: [ 40, 90],
5: [ 33, 112],
2: [ 0, 160],
3: [-50*np.cos(a), 160 + 50*np.sin(a)],
4: [-115, 160-70 ]},
7: {
1: [ 0, 160],
2: [250*np.sin(a), 160+250*np.cos(a)],
3: [250*np.sin(a)-50*np.cos(a), 160+250*np.cos(a)],
4: [-50*np.cos(a), 160+ 50*np.sin(a)]}
}
# Subdivisions to create within each block:
divs = {
1: (3,3),
2: (3,3),
3: (3,4),
4: (3,3),
5: (3,3),
6: (4,4),
7: (6,4)
}
def create_quads():
model = ops.Model(ndm=2, ndf=2)
model.nDMaterial("ElasticIsotropic", 1, 200e3, 0.25)
for num,block in blocks.items():
model.surface(divs[num],
element="quad", args=(1, "PlaneStrain", 1),
points = block)
return model
def create_tris():
model = ops.Model(ndm=2, ndf=2)
model.nDMaterial("ElasticIsotropic", 1, 200e3, 0.25)
elem = 1
for num,block in blocks.items():
# Because no element argument is passed, only nodes are created.
# Next we will go back over the newly created cells and manually
# create triangles.
mesh = model.surface(divs[num], points = block)
# For each new 4-node cell, create two triangles
for cell in mesh.cells:
nodes = mesh.cells[cell]
model.element("tri31", elem, (nodes[0], nodes[1], nodes[2]), 10, "PlaneStrain", 1)
model.element("tri31", elem+1, (nodes[0], nodes[2], nodes[3]), 10, "PlaneStrain", 1)
elem += 2
return model
def create_boundary(model):
# Load magnitude
P = 300
# Fix the first node, which is at (0.0, 0.0)
model.fix(1, 1, 1)
# Create a load pattern
model.pattern("Plain", 1, "Linear")
for node in model.getNodeTags():
coord = model.nodeCoord(node)
# Fix corner of block 4
if np.linalg.norm(np.array(coord) - blocks[4][4]) < 1e-12:
model.fix(node, 1,1)
# Add load to the corner of block 7
elif np.linalg.norm(np.array(coord) - blocks[7][3]) < 1e-12:
model.load(node, (P, 0), pattern=1)
def create_wrench(element="Quad"):
#model = create_quads()
if element == "Quad":
model = create_quads()
else:
model = create_tris()
create_boundary(model)
return model
if __name__ == "__main__":
model.analysis("Static")
model.integrator("LoadControl", 1)
model.analyze(1)
# Render the deformed shape
artist = veux.render(model, lambda i: [500*u for u in model.nodeDisp(i)])
veux.serve(artist)
References
- Logan, D.L. (2012) A First Course in the Finite Element Method. 5th ed. Stamford, CT: Cengage Learning.